|
|
|
NEW APPROACH TO LOGISTICS COSTS OF A FREIGHT FORWARDERS' COMPANY Andrzej Wartecki ABSTRACT In this paper we propose to describe a general method of dealing with line graphs of functions arising in economy such as stock exchange indices, prices, exchange rates etc. The se functions are implicit, this is to say, no analytic formula is given, only the line graphs are known. Although the technical and fundamental analysis developed various nice methods of identifying "patterns of changeability" of stock exchange indices, this is the first attempt to apply an idea of polish mathematician Stefan Banach back in 1925 to line graphs of functions with extensive use in logistics. Considering the most popular definition: "logistics costs is the overall expenditure pertinent to logistic processes which are ongoing in a company (logistics costs are expenses entailed by ongoing logistic processes and pertaining to: amortization, operation and exploitation of fixed assets in a logistic infrastructure, organization and physical flow management and storing of materials, semi-products (goods or wares), data management and data flow, remuneration of employees in logistics departments together with additional social security dues, fees etc., liabilities and commitments relevant to logistic processes, fuel, power, gas, materials and other outsourced services such as transport, refurbishment, overhauling, transports agency, customs, telecommunications, unaccountable damage due to logistic processes, negative impact on natural environment including exceeding of emission norms for poisonous or polluting substances, terrain damage, sewage and waste, exceeding levels of noise etc. (def. suggested by A. Wartecki) ), we can see that the following two aspects are of particular interest: identification and optimization of cost. The processes we are referring to are measured and controlled by the numerical data thus what we need most is their qualitative identification, by the way they are named in the book-keeping section, i.e. accounting instruments. The principal feature of the book-keeping work is the acquisition of full knowledge relevant to how where and when logistics cost come into existence and having them under complete control. If we want to diagnose and analyse the logistics activities we must run calculations and optimize them. Identification of costs in order to see what they have in common and where they differ is the main aspect of the analysis. While presenting our view in the table below we tried to generalize the dichotomy division: no semantic fields of the given items overlap and the list is complete, i.e. there are no other logistics specific items which might be quoted added to the list. Our table shows the way of viewing the identification problem of logistics specific costs in a freight forwarder's company. Following this proposal we are getting a basis for processing the data according to various criteria, for instance: time horizon, minimum value (price, cost) etc.
We apply the known statistical means to get estimations of such cost variables as fuel, oil and lubricants and operational cost in the years 2000 - 2002 (Figure 1). However, these methods are not sufficient to calculate and predict the share of each cost variable in the overall cost or know more about various economic measures in this respect. Our cost variables (also referred to as parameters) are time functions shown as line graphs, defined as sequences (sometimes very "long" ones) of ordered pairs of numbers which are simply real life data (this is what we see on Figure 2). We do not have an analytical formula to go by. Not surprisingly, the statistical means method shows that their lines of trends have the rising tendency - when mileage increases so do costs variables. However, two vital characteristics of the underlying cost variables are left out of this analysis: number of oscillations and the rate of increase (or decrease) of each monotonic piece of the line graph. If we are to learn more about behaviour of cost variables as functions of time we need a more powerful tool. This tool is called the "Banach indicatrix" or "multiplicity function". INTRODUCTIONRecall, a line graph is a specific subset of the Cartesian product of real lines R1 x R1 = R2, this is to say a set of points of the plane R2 of the form (x, f(x)), where x is an argument of a function and f(x) - its value. We usually have only a finite (though perhaps very large) number of such pairs. The Stefan Banach's idea allows us to discover and calculate many intrinsic characteristic features of any given (and drawn) function, in particular the classical economic measures of a company. The functions of bounded variation were introduced for the first time in connection with the theory of Fourier series and found later many generalizations in functional analysis. Definition: we call variation of a real function f defined on an interval <a, b> Var(f; a,b) = Sup ∑|f(ti ) - f(ti -1)|, where the supremum is taken over all partitions of the interval <a, b> (partitions are collections of non-overlapping subintervals: π: a = t0 < t1 <... tn-1 < tn = b. The variation can be easily calculated for simple functions (having finite set of values, piecewise constant), piecewise linear and monotonic. We have then Var(f;a, b) = f(b) - f(a), if for t1 ≤ t2 f(t1) ≤ f(t2) holds. This intuitive concept is very clear: variation "is summing up" all the "ups and downs" of a real function and if it is piecewise monotonic then its variation is equal to the sum of oscillations on each monotonic interval. However, it is not that easy to calculate the variation of any continuous function, even with few extremes. BANACH INDICATRIXLet f(x) be any real valued function defined on an interval <a, b> R2 ∋ (x,f(x)): x → f(x). Let us introduce the notation:
N(t, f) is called the Banach indicatrix [Banach 1925]. To put it less precisely and more understandably, the Banach indicatrix tells us how many times a given function f transforms arguments tk into a fixed value y=f(tk) or what is the number of elements in the set {(tk, f(tk): where f(tk) are equal}. The Banach indicatrix provides also a neat alternative to monotonicity or, as it is called in economics - trend. We simply call a function monotonic if it is N(f;) =1! The Banach indicatrix is a simple function and its values are natural numbers. VARIATION AND INDICATRIXIn 1936 Stefan Banach published the following THEOREM: A continuous function f(x) has bounded variation (i.e. Var(f;a,b) < ? ) if and only if its indicatrix N(t) is measurable in the sense of Lebesgue. Then there holds Var(f;a, b)) = -∞∫+∞N(t)dt INTERPRETATIONThe formula from the THEOREM enables us to calculate fairly easily and effectively the variation (which otherwise could be difficult). However, there remains the question how to deal with any f to calculate its N(t, f). We did it by hand but more busy logistics people are referred to where there is an algorithm and a piece of software able to compute the variation. Suppose we have this variation corresponding to some parameters - fuel, tyres, oil as functions of time. What makes it so special? Without the Banach indicatrix all we could do was to ask technical analysts for how long the current monotonic trend was going to last. If their methods consisting in identifying sequences of vertices of consecutive rising-falling patterns failed we would still be in the dark. Luckily, the Banach indicatrix never fails as far as these characteristics are concerned. We will get back to this topic later. For the time being let us recall a concept of norm from the functional analysis. Var(f;a,b) is a norm, this is to say, for every function defined on a finite interval and such that Var(f;a, b) < ∞ it verifies the following conditions I Var(f;a,b) = 0 if and only if f =0; II Var(kf;a,b) = k Var(f;a,b) where is a real number k>0; III Var(f + g;a,b) Var(f;a,b) + Var(g;a,b). With the use of the norm we can define another fundamental concept - the metric. It is a generalization of the classical concept of distance. A metric defines something like a distance between two elements regardless of the nature of these elements. We call metric any function d(f, g), where f, g are any elements (such as points or functions), which verifies the following conditions: a. d(f, g) = 0 if and only if f = g, b. d(f, g) = d(g, f), c. d(f, g) d(g, h) + d(h, f), where h is any element from the set where f, g belong. Now, let us put d(f, g) = Var(f - g;a,b). Once we have this, and our algorithm to compute there is a lot we can do: compute or just estimate the distance between line graphs, in other words see to what extent they differ or which of them is "smaller". There are other metrics likely to be of use for our purposes. Definition: put D(N)(f, g) = means {t: N(f; t) ≠ N(g, t)}. These ideas bring us to the question of interpretation of the Banach indicatrix as a characterization of a line graph. Roughly speaking, it is an intrinsic measure of the number of monotonic pieces a line graph of a function features. On the other hand N(f;t) gives an account of the frequency of occurrences of a function's values. This feature is directly related to weighed means. We could use them to get more information about its foreseeable behaviour. THE BANACH INDICATRIX COUNTWe are going to show a simple calculation of the Banach indicatrix for a line graph of fuel and oil consumption. On the chart below there are costs of these two parameters changing as a function of mileage and not time, we did this for simplicity. We are just counting "by hand" points where dotted horizontal lines cross the polygonal line. 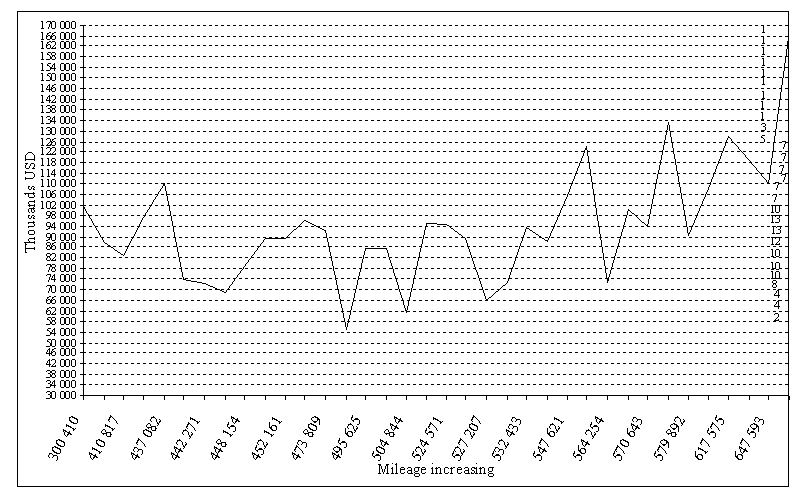
Fig. 1. Cost of fuel and oil consumption in 2000-2003 (USD)
Rys. 1. Koszt paliwa i oleju w latach 2000-2003 (USD) Now, values of this indicatrix can be written informally as follows Ind(N, f) = [2,4,4,8,10,10,10,12,13,13,10,7,7,7,7,7,7,5,3,1,1,1,1,1,1,1,1,1]. Strictly speaking, this is the image of variables indicated on the Y-axis (cost) through the indicatrix N(f, . ). Variables on the Y-axis are costs of fuel and oil. They are matched with results of the indicatrix count and shown in the table 2.
Now, we are looking for values where f(x) approach min. Let us see Figure 2. 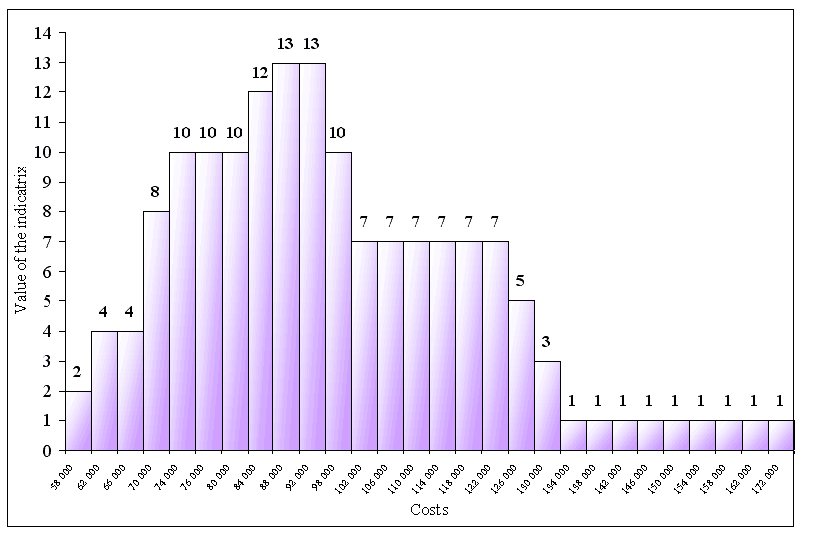
Fig. 2. Multiplicity of one-time value corresponding to many times variables
Rys. 2. Wielość pojedynczych wartość odpowiadających wielokrotnym zmiennym Let us notice the blue shaded surface under the graph of the indicatrix equals Var(c;<54.000, 134.000>), where c = c(miles) is the cost as function of mileage.Roughly speaking this chart is reminiscent of the Gauss normal density. However, since we are trying to find a rough estimate for costs reaching their minimum we must consider the indicatrix values to the left of the chart, this is to say Ind(N; f) = [2,4,4], which are corresponding to cost variable in the interval 58 000 to 66 000 USD and mileage from 482 976 to 527 207. We may conclude that the minimal cost does not happen very often. We are now in a position to tell what costs occur most frequently and this is our issue. In this way, managers of logistics will know what is the realistic level of their expectations as to cost. Our line of thought is the following. Once we have the indicatrix ready, it is possible to calculate the distance between line graphs to see where they differ and what they have in common. It is also possible to put cost variables in a sequence to see which is smaller or bigger. What we need now is optimization of cost on the basis of the Banach indicatrix analysis. We will get back to this point in subsequent papers [Ciemnoczołowski, Wartecki 2001]. REFERENCES
NOWE PODEJŚCIE DO KOSZTÓW LOGISTYKI PRZEDSIĘ-BIORSTWA PRZEWOZOWEGO
STRESZCZENIE W publikacji przedstawiony został funkcjonał - indykatrysa Banacha (1925) ze względu na jej zastosowanie do badania przebiegu zmienności funkcji (rzeczywistych), obejmujących także funkcje miar stosowanych w ekonomice przedsiębiorstwa takich jak, np.: stopa procentowa, notowania giełdowe, ceny, koszty, produkcja, rentowność, sprawność, przychody, itp. W/w właściwości (indykatrysy) umożliwiają dokonanie precyzyjnych obliczeń, które ułatwiają łatwe i szybkie ocenienie ważnych mierników ekonomicznych przedsiębiorstwa, jak również mogą być wykorzystane w procesie optymalizacji kosztów np. logistyki. Aspekty teoretyczne indykatrysy odniesione zostały do sfery praktycznych zastosowań, w których wykorzystano informacje ekonomiczne pochodzące z przedsiębiorstwa przewozowego. Stefan Banach (1892 - 1945) wybitny przedstawiciel lwowskiej szkoły matematycznej.
NEUER ANSATZ ZUR LOGISTIKKOSTEN VON TRANSPORT-UNTERNEHMEN
ZUSAMMENFASSUNG. Der Beitrag beschäftigt sich mit dem Banach Indikatrix im Zusammenhang mit dessen Anwendung zur Untersuchung des Verlaufs der Variabilität von Funktionen. Funktionen von Messgrößen, die in der Unternehmensökonomik Anwendung finden (Prozentsatz, Börsennotierungen, Preise, Produktion, Rentabilität, Einnahmen etc). Die genannten Eigenschaften ermöglichen die Durchführung präziser Berechnungen, die eine einfache und schnelle Beurteilung wichtiger ökonomischer Kennzahlen des Unternehmens gewährleisten. Diese Eigenschaften können auch bei der Kostenoptimierung (z.B. Logistikosten) verwendet werden. Theoretische Aspekte des Indikatrix beziehen sich auf praktische Anwendungen, wo ökonomische Daten aus einem Transportunternehmen genutzt wurden. Stefan Banach (1892 - 1945) - angesehener Vertrter Lemberger mathematischen Schule.
Andrzej Wartecki |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Copyright © 2005 LogForum, Wyższa Szkoła Logistyki, ul.E.Estkowskiego 6, tel. 061 852 95 55, 851 06 04, tel./fax. 061 851 06 03 |
