GENETIC ALGORITHMS FOR 3D PACKAGING PROBLEMS IN FOOD INDUSTRY

Semih Ötleş, Mustafa Murat Inceoglu, Korhan Karabulut, Ata Önal
Ege University, Izmir, Turkey

ABSTRACT

Packaging problems arise in many industries. Nowadays, with ever growing international trade, transportation costs directly affect the profits. Efficient packing is very important because even reduction a few wasted cm³s of a container can save a lot of money. This work is about a sample packaging problem in food industry. A previously introduced general-purpose method called DBLF (deepest bottom left fill) is applied to a set of problems and the results are presented. Up to 98% utilization is obtained.

Key words: packing, container, transportation.

INTRODUCTION

Containerization in food industry is a system of intermodal cargo. Cargo is a term used to denote foods and other products or produce being transported generally for commercial gain, usually on a ship, plane, train or lorry. Advances in transportation technology of food industry have made it possible for shippers to deliver perishable food products to purchasers thousands of miles away with no substantial loss in freshness and quality and at lower and lower costs.

The usage of containers shows the complementarity between freight transportation modes by offering a higher fluidity to movements and a standardization of loads. Its rectangular shape is can easily be handled, making the container a convenient tool for transhipment activities. There are three common standard lengths, 20 ft, 40 ft and 45 ft. Container capacity (of ships, ports, etc) is measured in twenty-foot equivalent units (TEU). A TEU is a measure of containerized cargo equal to one standard 20 ft (length) x 8.5 ft (height) container (approx. 40.92 m³). Most containers today are of the 40-ft variety and thus are 2 TEU. 45-ft containers are also designed 2 TEU. Two TEU are referred to as one FEU (forty-foot equivalent unit). These two terms of measurement are used interchangeably. High-cube containers have a height of 9.5 ft, while half-height containers, used for heavy loads, have a height of 4.25 ft. It can transport a wide variety of foods ranging from raw materials (rye, wheat), manufactured foods to frozen food products. There are specialized containers for transporting liquids (oils) and perishable food products (called "reefers" which now account for 50% of all refrigerated cargo being transported).

Optimization of containers built in distribution across cartons, pallets and trailers gives the freedom to lower the shipping costs per unit by loading more cargo per container or trailer. By optimizing the loads, the organization can ship fewer loads using more efficient loading patterns. By optimizing the load patterns, the costs associated to damaged cargo can be eliminated. Companies are increasily looking for tools that will help them optimize distribution performance. Generally, all described algorithms carry out (repetitively) first the statistically optimized preliminary sortings (with some additional aid of a kind if so called "genetic algorithms", and than a quick geometric procedure for compact arrangement of the formed queue of 2D rectangular parts (or 3D boxes) of arbitrary sizes into the 2D sheet (3D container) under the condition known as "bottom left" rule i.e. minimizing x, y, z - coordinates in consequence for each next part in the queue, or under any analogous rule. In this paper, a hybrid genetic algorithm (GA) was used for container loading for industrial food products.

GENETIC ALGORITHMS

Genetic algorithms are general-purpose artificial intelligence methods based on the simulation of the natural evolution. Genetic algorithms are first introduced by Holland in 1975 [Holland, 1975] and are studied by many researchers. The building blocks or elements in genetic algorithms are "individuals" which are candidate solutions for a problem. Each of the individuals is called either a "genotype" [Holland, 1975] or a "chromosome" [Schaffer and Eshelman, 1987].

A genetic algorithm is an iterative process and is composed of several steps. Generally, a random initialization is step is required. Then a "fitness score" is assigned to each individual according to how good it fits as a solution to the problem. A "fitter" or better individual is given a higher score. Then, each individual is given a chance to "reproduce". While fitter individuals have higher chances to reproduce, less fitting elements still have a smaller chance. Several individuals are selected randomly from the new population to mate through a process called "crossover". This produces new children (or off-springs) with some features inherited from each parent. After recombination, a mutation operator can be applied. Each bit in the population can be mutated (flipped) with a low probability generally smaller than 1%.

A good GA will converge to an optimal solution after several iterations. Genetic algorithms are not guaranteed to find the global optimum solution to a problem but they are generally good at finding "acceptably good" solutions to problems "acceptably quickly" [Beasley et.al., 1993].

Typical applications of genetic algorithms are numerical function optimization, scheduling, game playing, adaptive control, transportation problems, travelling salesman problems, bin packing, time tabling, etc.

DBLF AND 3D BIN PACKING

Bottom Left (BL) and Bottom Left with Fill (BLF) methods are used in 2D bin packing. In BL, introduced by Jakobs [Jakobs, 1996], each item is moved as far as possible to the bottom of the object and then as far as possible to the left. BL is relatively a fast algorithm with complexity O(n²). The major disadvantage of the method is; empty areas in the layout are generated. Hopper (Hopper, 2000), to overcome this disadvantage, develops the BLF algorithm. This algorithm allocates each object to the lowest possible region of the bin thus fills the empty areas in the layout. The major disadvantage of this algorithm is its O(n³) complexity.

Deepest BLF is an extension of the BLF method to cover 3D bin packing problems [Karabulut and Inceoglu, 2004]. An object is moved to the deepest available position (smallest z value) in the layout, and then as far as possible to the bottom (smallest y value) and then as far as possible left (smallest x value).

Since the complexity of the BLF algorithm is high, a computer efficient implementation of this algorithm is needed. Below is the Deepest BLF algorithm used in this work.

In the beginning, the empty list has only one empty volume with dimensions same as the bin. As the algorithm iterates, new empty volumes are added to the list. The next box from the list is chosen to work on. Then each position in the list is checked to see if the current box fits in. If the empty volume is large enough, the position is checked for intersection with other boxes that were placed before. This check is needed because for an efficient implementation, all the volumes in list are not up to date. If there is no intersection at the chosen position, the box is inserted at this position and is iterated to the deepest bottom left position. Then the position list is updated and checked to see if there is any unnecessary position. In the final step, the new list is sorted in deepest bottom left order. Then the next box is taken from the list and the same selection procedure is repeated. Also as an additional constraint, the boxes are not allowed to rotate.

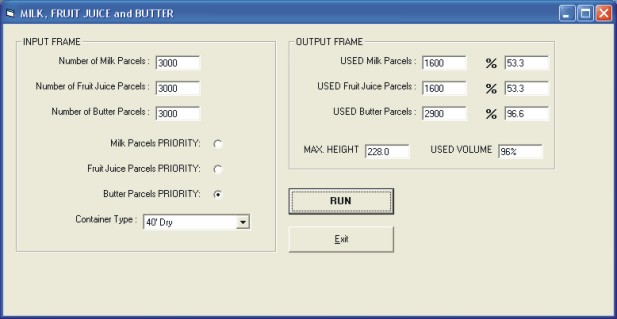
RESULTS

DBLF algorithm has been written in C++ programming language on Windows operating system and has been tested on Pentium-4 based computer. This computer has 2.4 Ghz processor and 1024 Mbytes memory. In order to facilitate data entering, a user interface has been developed (Figure 1).

This computer program has been tested various 20' and 40' container types and has been optimized to load milk, fruit juice and butter boxes into container. This program has been used DBLF algorithm to load boxes into container. The highest point of the boxes has been compared the highest point of the container and decided to stop or continue to program. In this case, the boundary value of the problem is the minimal volume of the container is 90% full.

In Table 1, various 20', 40' containers and their dimensions are shown.

	Fig. 1. User interface Rys. 1. Interfejs użytkownika

In Table 2, milk, fruit juice, butter boxes and their dimensions are shown.

Firstly, computer program has been run for 2000 milk, 2000 fruit juice and 2000 butter boxes. This program has a priority-based selection mechanism that the user can select a special box (for example fruit juice boxes) to fill the container volume in order of priorities. In Table 3, for 20' container has 238.0 cm maximum height has been used, first line has butter boxes priority results, second line has fruit juice boxes priority results and last line has milk boxes priority results are shown. In this table (for example first line), 80% of butter boxes for butter boxes priority are filled to container and 98% of the container volume has been used.

In order to reduce the amount of computer running time, boxes have been filled groups of 50. In another experiment, computer program has been run for 3000 milk, 3000 fruit juice and 3000 butter boxes using 40' dry container. The results are shown in Table 4.

In Table 3 and Table 4, the maximal number of butter, fruit-juice and milk boxes are located to the container. This program has been filled firstly milk boxes (for example, milk boxes has priority) and than the smallest boxes (for example, butter boxes) has been located to the container.

DISCUSSION

In this study, a genetic algorithm has been developed for milk, fruit-juice and butter boxes located into 7 different types of containers. Genetic algorithm has been used deepest bottom left fill (DBLF) method. Up to 98% utilization is obtained and container volumes are at least 92% filled of boxes.

REFERENCES

Beasley D., Bull D.R., Martin R.R., 1993. An Overview of Genetic Algorithms: Part 1, Fundamentals. University Computing, 15(2), 58-69.

Holland J.H., 1975. Adaptation in Natural and Artificial Systems, MIT Press.

Hopper E., 2000. Two-dimensional Packing Utilising Evolutionary Algorithms and other Meta-Heuristic Methods. A Thesis submitted to University of Wales for the Degree of Doctor of Philosophy.

Jakobs S., 1996. On Genetic Algorithms for the Packing of Polygons. European Journal of Operational Research, 88, 165-181.

Karabulut K., Inceoglu M.M., 2004. A Hybrid Genetic Algorithm for Packing in 3D with Deepest Bottom Left with Fill Method. Lecture Notes in Computer Science, 3261, 441-450.

Schaffer J.D., Eshelman L., 1987. Some Effects of Selection Procedures on Hyper-plane Sampling by Genetic Algorithms. Genetic Algorithms and Simulated Annealing.

ALGORYTMY ROZWIĄZAŃ DLA PROBLEMÓW PAKOWANIA PRZESTRZENNEGO W PRZEMYŚLE SPOŻYWCZYM

STRESZCZENIE Problemy związane z pakowaniem występują w wielu gałęziach przemysłu. Obecnie, przy coraz istotniejszym udziale handlu międzynarodowego, koszty transportu bezpośrednio wpływają na zyski. Efektywne pakowanie jest bardzo ważne, gdyż redukcja nawet kilku zbędnych cm³ kontenera może zaoszczędzić wiele pieniędzy. Praca przedstawia przykładowy problem związany z pakowaniem w przemyśle spożywczym. Wcześniej już omawiana metoda DBLF (wypełniane najgłębiej na dole od lewej) została zastosowana i jak przedstawiają uzyskane wyniku, uzyskano wykorzystanie przestrzeni aż do 98%.

Słowa kluczowe: pakowanie, kontener, transport.

ALGORITHMEN FÜR DIE PROBLEMLÖSUNG IM BEREICH DER DES 3D PACKAGING IM LEBENSMITTELINDUSTRIE

ZUSAMMENFASSUNG. Probleme des Verpackens treten in vielen Industriezweigen auf. Aktuell, bei dem wachsenden Anteil des internationalen Warenverkehrs werden Gewinne durch Transportkosten direkt beeinflusst. Effektives Verpacken ist daher von großer Bedeutung, denn durch die Reduzierung von sogar einigen unnötigen cm³ des Containers kann viel Geld erspart werden. Die vorher erörterte DBLF Methode wurde implementiert und - wie dies die ermittelten Ergebnisse nachweisen - die Nutzung des Containerraums sogar bis auf 98% erreicht.

Codewörter: Verpacken, Container, Transport

Semih Ötleş
Department of Food Engineering
Ege University
Bornova 35100 Izmir, Turkey
e-mail: semih.otles@ege.edu.tr

Mustafa Murat Inceoglu, Korhan Karabulut, Ata Önal
Dept. of Computer Eng.
Ege University
Bornova 35100 Izmir, Turkey